by Wesley Collier and Natasha Schmitz.
Abstract
As a study of quantum chemistry calculations, AM-1, 3-21G, 6-31G,and double zeta valence basis sets were used to calculate energy optimized geometry vibrational frequencies, potential energy vs. bond stretch, dipole moment, and uv/vis spectra on hydrobromide, difluoroamine, and ethylbenzene. Comparison with the literature shows some strong agreements and some strong disagreements, with values of geometry being the most accurate and uv vis and vibrational frequencies being the furthest from measured values.
Introduction
Solutions to the Schroedinger wave equation continue to promise unparalleled knowledge about chemical structure and properties. In the past two decades, computer processing power has increased to the degree that sophisticated computations may be performed on the typical home computer. Software packages available from consumer to student to professional levels are affordable. However, the solutions produced by these methods, while often accurate, are dubious at best and absurd at worst.
A wavefunction is able to be expressed as the sum of multiple wavefunctions, and the strategy is to start with a product of many potentially accurate wavefunctions. The more potential wavefunctions we can start with, the more accurate the results are. Therefore the accuracy of the solutions is limited only by our ability to solve the wave equation. To that end a comparison of the computation results to experimental measurements is given in terms of vibrational frequencies, potential energy vs. bond stretch, dipole moment, and uv/vis spectra on hydrobromide, difluoroamine, and ethylbenzene.
Experimental
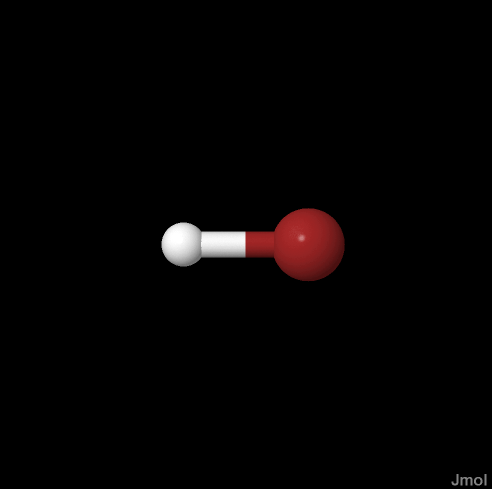
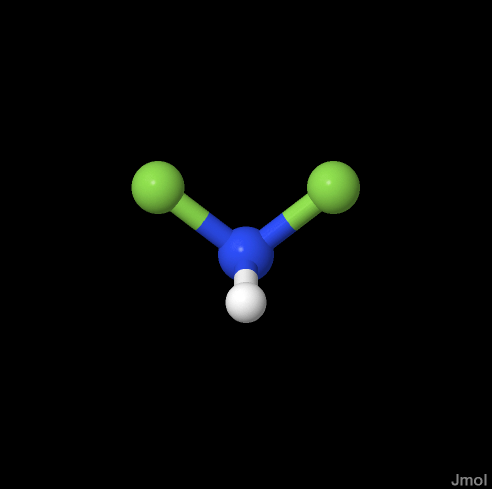
Data was generated for hydrobromic acid, difluoroamine, and ethylbenzene. On a web based computation server, WebMO running GAMESS, the initial geometry optimizations were performed by the semi-empirical MOPAC method using AM-1 basis sets for HNF2 and ethylbenzene. A minimal basis set was chosen for HBr after multiple failed attempts to optimize geometry. The optimization was based on measured force constants (Hooke’s Law), and the calculation proceeded by guessing a geometry and then observing the energy of the arrangement. The rate of change of the energy with respect to each of the parameters was observed over the parameter domains and used to choose the lowest energy arrangement.
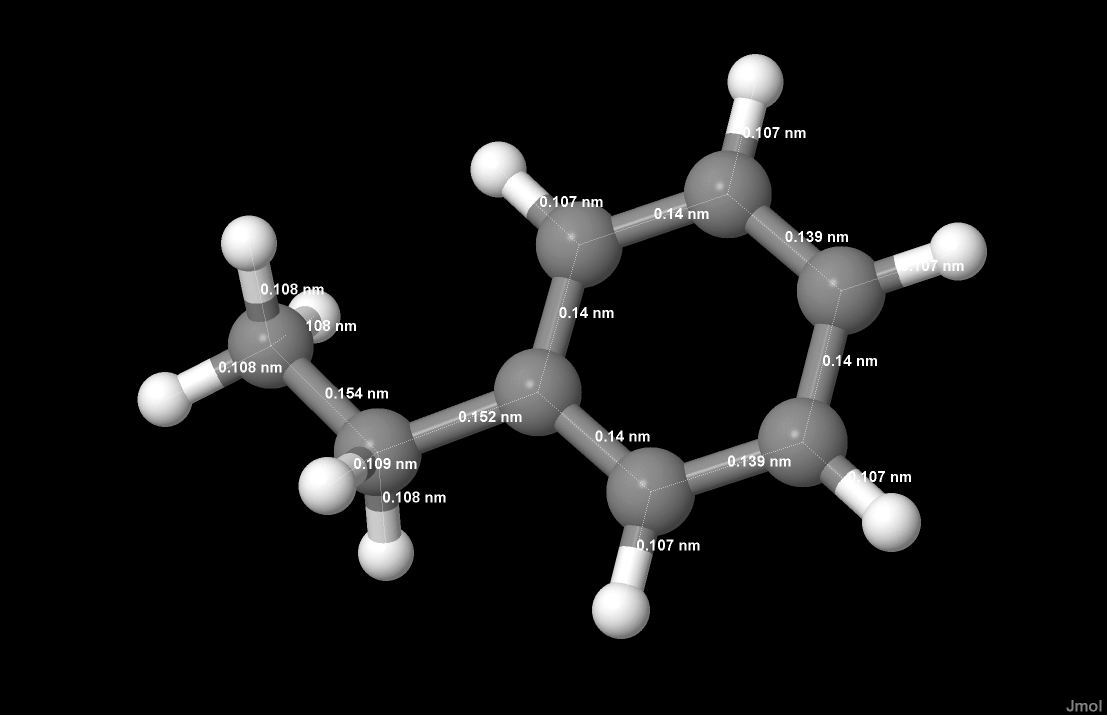
Once the geometry was optimized using the WebMO server, the data was imported into Macmolplt which in turn wrote an input file specifying the type of calculation, basis set choice, etc. A software package called GAMESS used the input file to further optimize the geometry using successively larger basis sets. In order of increasing size, the basis sets used were AM-1, 3-21G, 6-31G, and double zeta valence. The succession allowed us to see the effect of using a larger basis set on the output data.
Conclusion
Looking over the data provided and comparing it to the literature values some observations can be made. The calculations concerning bond lengths and angles all seemed to be fairly accurate. The displays of the various atoms structures also seem to be what one would normally expect of them. Some of the calculations that did not work as well in this experiment included the UV-vis calculations. Most of these for the ethylbenze were off far from the literature values collected. This could have been a factor of the geometry not fully optimizing or other computational errors. Overall these types of calculations are very useful, but one has to be careful of what types of calculations are being done, and making sure everything is run to the best possible geometries.
As a study of quantum chemistry calculations, AM-1, 3-21G, 6-31G,and double zeta valence basis sets were used to calculate energy optimized geometry vibrational frequencies, potential energy vs. bond stretch, dipole moment, and uv/vis spectra on hydrobromide, difluoroamine, and ethylbenzene. Comparison with the literature shows some strong agreements and some strong disagreements, with values of geometry being the most accurate and uv vis and vibrational frequencies being the furthest from measured values.
Introduction
Solutions to the Schroedinger wave equation continue to promise unparalleled knowledge about chemical structure and properties. In the past two decades, computer processing power has increased to the degree that sophisticated computations may be performed on the typical home computer. Software packages available from consumer to student to professional levels are affordable. However, the solutions produced by these methods, while often accurate, are dubious at best and absurd at worst.
A wavefunction is able to be expressed as the sum of multiple wavefunctions, and the strategy is to start with a product of many potentially accurate wavefunctions. The more potential wavefunctions we can start with, the more accurate the results are. Therefore the accuracy of the solutions is limited only by our ability to solve the wave equation. To that end a comparison of the computation results to experimental measurements is given in terms of vibrational frequencies, potential energy vs. bond stretch, dipole moment, and uv/vis spectra on hydrobromide, difluoroamine, and ethylbenzene.
Experimental
Data was generated for hydrobromic acid, difluoroamine, and ethylbenzene. On a web based computation server, WebMO running GAMESS, the initial geometry optimizations were performed by the semi-empirical MOPAC method using AM-1 basis sets for HNF2 and ethylbenzene. A minimal basis set was chosen for HBr after multiple failed attempts to optimize geometry. The optimization was based on measured force constants (Hooke’s Law), and the calculation proceeded by guessing a geometry and then observing the energy of the arrangement. The rate of change of the energy with respect to each of the parameters was observed over the parameter domains and used to choose the lowest energy arrangement.
Once the geometry was optimized using the WebMO server, the data was imported into Macmolplt which in turn wrote an input file specifying the type of calculation, basis set choice, etc. A software package called GAMESS used the input file to further optimize the geometry using successively larger basis sets. In order of increasing size, the basis sets used were AM-1, 3-21G, 6-31G, and double zeta valence. The succession allowed us to see the effect of using a larger basis set on the output data.
Conclusion
Looking over the data provided and comparing it to the literature values some observations can be made. The calculations concerning bond lengths and angles all seemed to be fairly accurate. The displays of the various atoms structures also seem to be what one would normally expect of them. Some of the calculations that did not work as well in this experiment included the UV-vis calculations. Most of these for the ethylbenze were off far from the literature values collected. This could have been a factor of the geometry not fully optimizing or other computational errors. Overall these types of calculations are very useful, but one has to be careful of what types of calculations are being done, and making sure everything is run to the best possible geometries.
Click the Molecules!
| Hydrogen Bromide | Difluoroamine | Ethylbenzene |
 |  |  |