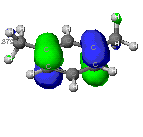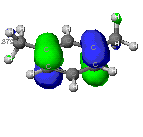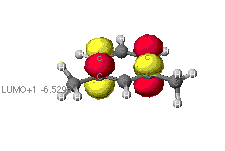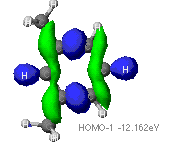Theoretical Calculations of Properties of m-Xylene
by Stacy Mundschau
Types of calculations performed
To generate the molecules shown below, three separate calculations involving
the molecular orbitals and their associated electrons were performed by
CAChe software. Due to the complexity involved in describing these shapes
mathematically, assumptions concerning the extent to which these orbitals
interact had to be made. Each set of assumptions, refered to as the Extended
Huckel, MOPAC or ZINDO, varies in the treatment of these interacting, or
overlapping, orbitals. While providing a simple method to generate molecular
values, the Extended Huckel theory can not match the agreement that MOPAC
and ZINDO calculations have with values determined in the laboratory. The
degree to which each theory accounts for the overlap between molecules
is a result of their dependence on a field of science known as quantum
mechanics. Particles decribed by quantum mechanics exist at the atomic
level (i.e electrons) and do not behave like the macroscale objects we
encounter. The superior accuracy of the ZINDO and MOPAC models is thus
a result of their reliance on quantum mechanical based modeling. the ZINDO
and MOPAC models relied on empirical data gathered from spectroscopy studies.
Results of geometry optimization at various levels of theory
The following depictions of m-xylene are based on the types of molecular
orbital calculations performed.
While the figures above look very similar, the assumptions underlying
each of the associated calculations can result in drastic differences in
the molecule's structure. The Extended Huckel theory treats molecules as
the familar balls linked to one another with sticks. The geometry the molecule
is governed by the bonds between balls acting as stiff springs. ZINDO and
MOPAC use the principles of quantum mechanics to determine the most likely
shape of the model, based on the lowest calculated energy value. This results
in a much more complete mathematical treatment of the molecule, and thus
provides more accurate molecular property values and depictions.
The molecular orbitals that provide the primary bonding
Not all of the molecular orbitals calculated by each model contribute equally
to the overall properties of m-xylene. Each theory's calculations essentially
"weight" the significance of each orbital. The orbitals selected below
are by no means all of the molecular orbitals that exist. However, their
low energy provides a more stable environment for electrons to exist and
interact with neighboring nuclei and electrons. Selected bonding orbitals
of the aromatic ring found using ZINDO calculations are provided below.
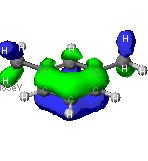
The highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals
The identification of the HOMO and LUMO molecular orbitals are critical
in understanding the manner in which a chemical reaction takes place. As
these are the sites which contain the most energetically unstable electrons
(HOMO) or are most willing to accept electrons (LUMO), It follows that
these are the orbitals most involved in chemical reactions . A redox reaction
can be used to illustrate the importance of HOMO and LUMO orbitals. Consider
the process of rusting in which neutral iron loses electrons to oxygen.
More specifically, the redistrubution of electrons from the HOMO orbital
of iron atom to the LUMO orbtial of oxygen weakens the bonds between oxygen
atoms. The decreased bond strength between oxygen atoms drives the cleavage
of the oxygen molecule and the simultaneous oxidation of iron. In addition
to explaining reactions, identifying HOMO and LUMO orbitals can be used
to predict if a proposed reaction will occur.
Electron density/distribution maps
In addition to determining the shape and energies of the molecular
orbitals, each theory is able to model how the electrons will arrange themselves
over the molecule. That is, these calculations will show where the electrons
will most likely be in a concerted effort to lower the overall energy of
the molecule. The left diagram of m-xylene shows the relative uniformity
of electron density through out the aromatic ring. Recall that aromatic
rings are molecules commonly represented by rings whose double bonds "flip"
or resonate to alternating positions in the molecule. The diagram on the
right shows the electron deficent regions on the methyl groups hydrogens.
As electrons carry a negative charge, the increased probability that they
will be found in a certain region results in a localized polarization of
the molecule.
(this space contained an image of
Nitrobenzoic acid by mistake) |
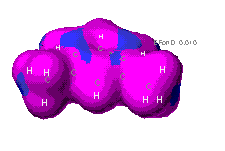
Image of m-xylene |
Charge distribution maps
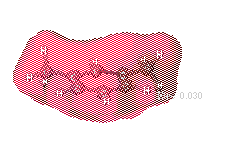
This tendency of electrons to polarize certain regions of the molecules
allows for the intramolecular (inside of the molecule) charge to be depicted.
It is important to mention that the prescece of negatively charged regions
requires that equally postive charged regions must exist if the overall
molecule is going to remain neutral.
|
So why does electron redistribution to certain regions
of the molecule result in lower energies than in other arrangements? Essentially
what accounts for this hoarding of electrons into specific regions is a
property of individual atoms known as electronegativity. The tendency of
electrons to gather near highly electronegative atoms is explained by the
strength of attraction to its nucleus. Small molecules with few electrons
"shielding" other electrons from its nucleus give rise to the most electronegative
atoms. This pattern is reflected in the general increase of electronegativity
moving up the periodic table and to the right (excluding the noble gases)
The partial atomic charge, or the charge that each atom within a molecule
experiences, is determined by the electronegativities of its neighbors. |
As m-xylene contains no atoms that are particularly electronegative compared
to the neighbors, the partial atomic charge is relatively uniform throughout
the molecule. This is shown by the continuous red cloud surrounding the
xylene molecule.
Calculated dipole moments
By determing the molecular orbitals and regions of charge distribution
through mathematical models, calculating overall the dipole moment of the
molecule is possible. The dipole moment is a vector that shows how the
charge is distributed in a molecule. It can be thought of as the net sum
of the individual dipoles within the molecule. The following table lists
the dipole moment values calculated by the type of model structure.
| Ext.ended Huckel |
0.711 |
| ZINDO |
0.517 |
| MOPAC |
0.254 |
The Handbook of Chemistry and Physics lists ortho xylene's dipole moment
as 0.640.