The geometry optimizations for the three highest level of theory are shown. The bond angle of oxygen is 180 degrees and not included for this report. The literature value for the bond length of oxygen was 1.2075 angstroms.² The calculated values for each theory were the same and gave an error of 6.00%.

6-21G was the lowest level of theory used for geometry optimization.

6-31G was the next highest level of theory for geometry optimization.

Double Zeta Valence was the highest level of theory used for geometry optimization.

This is the highest occupied molecular orbital at orbital eight. The orbitals were determined by totaling the number of electron in the molecule and dividing by two.

This is the lowest occupied molecular orbital at orbital nine. This orbital would be the next occupied if the molecule were excited with an adequate amount of energy.

The partial atomic charge for a diatomic molecule is zero, which is shown here. They are created by the asymmetric distribution of electrons in a chemical bond; diatomic molecules have symmetric distributions because of equivalent electronegativities.

Table and Figure 1 below show the different orbitals for the O₂ molecule starting with the S sigma bonding orbitals and going down to the highest energy orbitals. The two P orbitals represent the p_x and p_y orbitals that contribute to pi bonding.


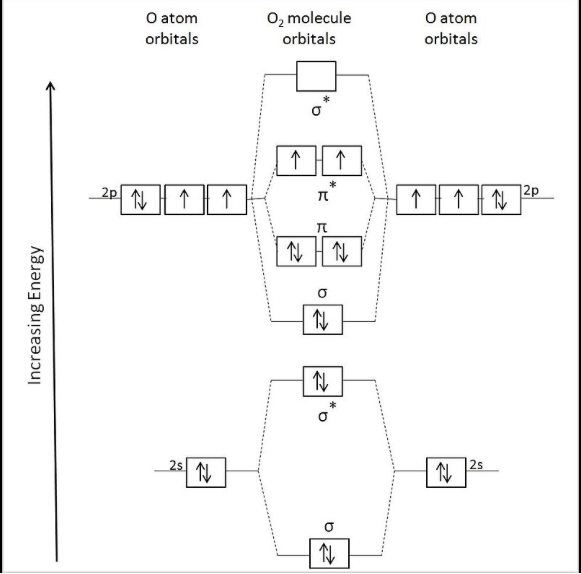
Figure 1: Orbital diagram showing the participating atomic orbitals from each oxygen atom, the molecular orbitals that result from their overlap, and the Aufbau filling of the orbitals.³

Table 1: Orbitals corresponding to the type of bonding occurring at that level.

Type of Bonding	Orbital
S sigma bonding
S sigma anti-bonding
P  bonding
P anti-bonding
P2 bonding
P2 anti-bonding

The different potential energies of bond stretching at different levels of theory are shown in Figure 1. The higher the level of theory, the lower in energy the theory calculates for the lowest potential energy. The bump in the graph is due to the interactions between electrons that are not accounted for in the theories. An experimental graph of potential energy would not have these bumps.


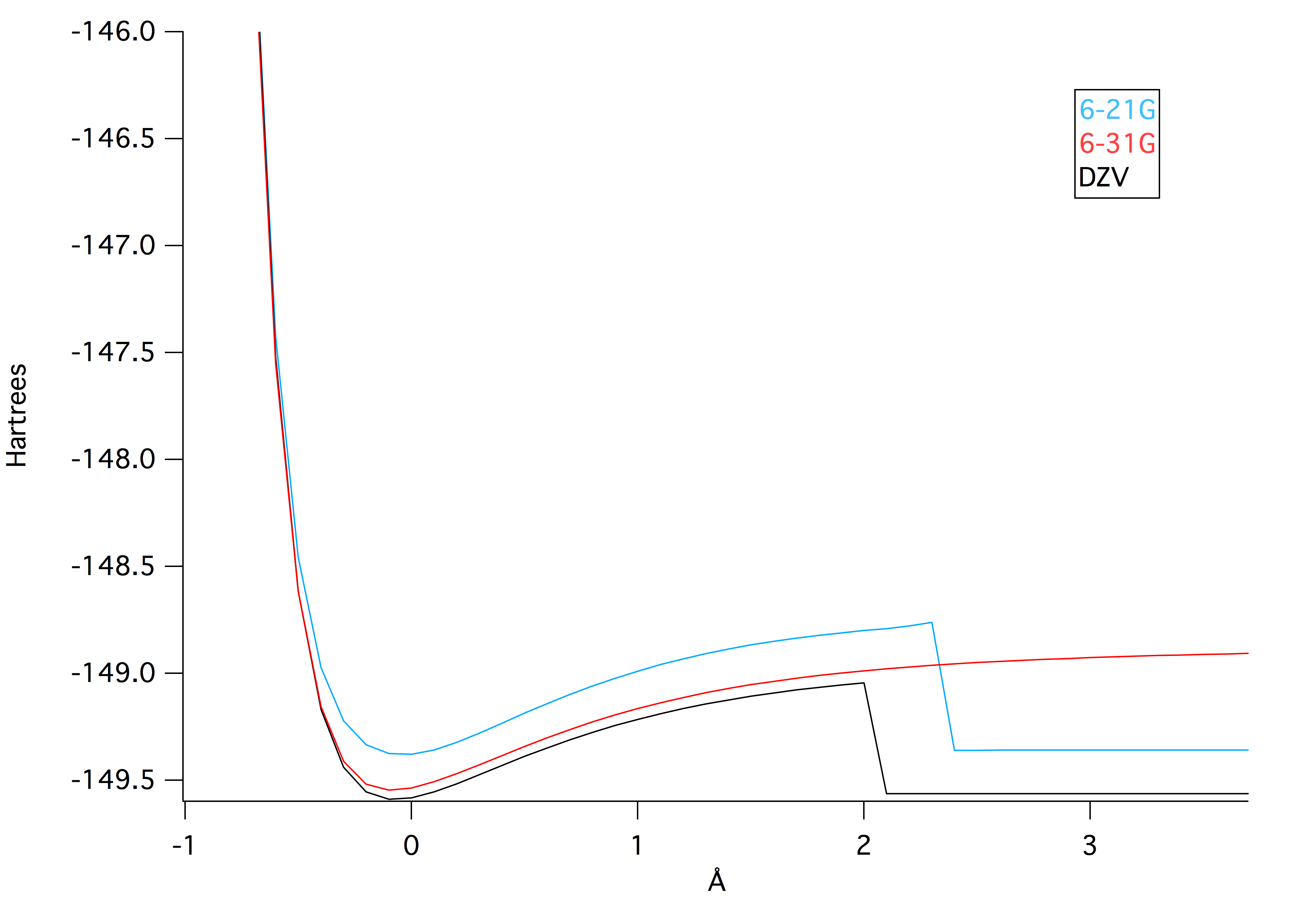
Figure 2: Potential energy (Hartrees) curves at different levels of theory plotted against bond lengths (angstroms).⁴

The vibrational frequency using DZV theory was 1364.52 cm^-1. In comparison to the NIST database value, 1580  cm^-1, there was a 13.6% error.²

You may look at any of these intermediate views again by clicking on the appropriate button.