Hydrogen Sulfife

Widgets will appear here

-Hydrogen Sulfide-

Hydrogen sulfide is a small polar molecule which exists as a colorless, flammable and toxic gas. This foul smelling compound occurs naturally in petroleum sources and in volcanic terrain. The molecular geometry of hydrogen sulfide resembles the bent geometry seen in water molecules.
To theoretically calculate the geometry of this molecule, The Hartree Fock self consistent field (HF-SCF) method was applied using increasing basis sets. Starting with a MOPAC basis set (AM-1), and feeding the lowest energy geometry into the next largest basis set (AM-1 -> 621-G -> 631-G -> DZV), the molecular dimensions were calculated at these different levels of theory.

Table #1: Calculated Molecular dimensions of different basis sets

	H-S-H bond angle (degrees)	S-H bond length (nm)
AM-1	95.1	0.132
621-G	96.1	0.135
631-G	96.2	0.135
DZV	96.2	0.135
Literature¹	93.3	0.13455

By observing table #1, as the basis set size increased, the bond length between the sulfur and the hydrogen approached the literature value of 0.13455nm showing that the Double Zeta Valence (DZV) basis set yielded the lowest energies at that atomic distance. However, as the basis set increased the bond angle began to deviate slightly more than the literature angle of 93.3 degrees.

To view the animations generated after each different HF-SCF basis set iteration, and to view the computer calculations of the bond lengths and angles, click on the buttons below to toggle between different basis set renderings.

---Molecular Surfaces---

Using the optimized geometry from the DZV basis set, various renderings were generated describing the physical properties of the molecule.

The molecular orbitals for hydrogen sulfide were generated. The Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO) were rendered, and their placement on the molecule can be seen by clicking the buttons below. Note that the different colors of the orbitals (red and blue) indicate the parity of the orbitals, and can be thought of as the + or - seen in two dimensional pictures.

A surface of the molecular electrostatic potential was also applied to the molecule to iterate the difference in charge density. The standard unit of electric potential is the volt, but here the concept is purely to iterate the spatial charge separation in the molecule as a consequence of electronegativity and atomic orbital energy levels. The red color indicates the enhanced presence of electrons in that region, and therefore a higher negatively charged zone. To see the colorful rendering of the electrostatic potential, click the button below.

The imbalance of electrons seen in the electrostatic potential lead to the nuclei within the molecule carrying partially positive or partially negative
charges. the button below will show a live picture with values for these partial charges.

Another consequence of the imbalance of electrons is the presence of dipoles within the molecule, and a total molecular dipole. Molecular dipoles were calculated using all three basis sets. However, the sulfur atom has available unoccupied d orbitals which electrons may disperse into; to account for this phenomenon in this theoretical calculation, additional diffuse d functions were added to the calculation to replicate the natural dispersion of the electrons. Dipole moments calculated in these trials are reported in table #2.

Table #2: Calculated Molecular Dipoles

Basis set used (# diffuse functions)	Dipole moment (Debeye)
AM-1	1.859680
621-G	1.850457
631-G	1.866086
DZV	1.844673
DZV (1S,1D)	1.375594
DZV (2S,2D)	1.1536603
DZV (3S,3D)	1.038927
Literature¹	0.970

Using the non-diffused basis sets, the calculations yield dipole moments that are significantly higher than the literature values, but as more and more diffuse functions were added, and the spatial distribution of the electrons began to resemble a nuclei with available d orbitals, the dipole moment began to get much closer to the excepted value. The DZV data set with 3 diffuse D functions and 3 diffuse S functions had the closest dipole moments with respect to literature values.

--Vibrational Modes of Hydrogen Sulfide--

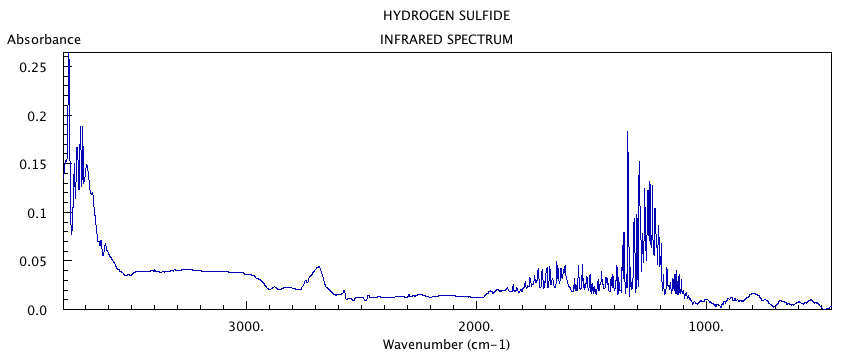
Finally, the energies between the vibrational molecular transitions were calculated using the DZV basis set, and the corresponding wavenumber was assigned to each transition. Three primary vibrational transitions were calculated in this molecule: at 2700cm-1, asymmetrical stretch is observed; at 2650cm-1, a symmetrical stretch is observed; at 1320cm-1, "scissoring" is observed in the molecule. These modes also show up as peaks in the infrared spectra for hydrogen sulfide as seen in figure #1. To see animations of each stretching mode, click the buttons seen below the infrared spectra.

Figure #1: FT-IR Spectra of Hydrogen Sulfide²

--References--

1) Lide,D.R.,Kehiaian,H.V. CRC Handbook of Chemistry and Physics; CRC Press, Boca Raton, FL, 1973; Sec F, pg 219, Sec E, pg 63.

2) NIST Standard Reference Database, 2013, accssed Mar, 5, 2013. http://webbook.nist.gov/cgi/cbook.cgi?ID=C7783064&Mask=80#IR-Spec

Page skeleton and JavaScript generated by export to web function using Jmol 12.2.34 2012-08-09 20:37 on Feb 26, 2013. "we got this sh** dialed in"

Using directory /Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide
  adding JmolPopIn.js
  ...jmolApplet0
      ...adding Optimized_Geometry_using_AM1.png
      ...copying
./Jmol.js
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/Jmol.js
      ...copying
./JmolApplet.jar
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/JmolApplet.jar
      ...copying
file:/Users/student2/Desktop/SK, AO/H2S/AM1/H2S-AM1-geoopt.log
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/H2S-AM1-geoopt.log
      ...adding Optimized_Geometry_using_AM1.spt
  ...jmolApplet1
      ...adding Optimized_Geometry_using_621-G.png
      ...copying
file:/Users/student2/Desktop/SK, AO/H2S/621G/H2S621.log
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/H2S621.log
      ...adding Optimized_Geometry_using_621-G.spt
  ...jmolApplet2
      ...adding Optimized_Geometry_using_631-G.png
      ...copying
file:/Users/student2/Desktop/SK, AO/H2S/631G/h2s631.log
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/h2s631.log
      ...adding Optimized_Geometry_using_631-G.spt
  ...jmolApplet3
      ...adding Optimized_Geometry_using_DZV.png
      ...copying
file:/Users/student2/Desktop/SK, AO/H2S/DZV/H2SDZV.log
         to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/H2SDZV.log
      ...adding Optimized_Geometry_using_DZV.spt
  ...jmolApplet4
      ...adding HOMO_orbital.png
      ...adding HOMO_orbital.spt
  ...jmolApplet5
      ...adding LUMO_orbital.png
      ...adding LUMO_orbital.spt
  ...jmolApplet6
      ...adding Electrostatic_potential.png
      ...adding Electrostatic_potential.spt
  ...jmolApplet7
      ...adding Partial_Atomic_Charges.png
      ...adding Partial_Atomic_Charges.spt
  ...jmolApplet8
      ...adding Molecular_Vibration_at_2700_Wavenumbers.png
      ...copying
file:/Users/student2/Desktop/SK, AO/H2S/DZV/H2S_DZV_vib.log
         to
      ...compressing large data file to
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/H2S_DZV_vib.log.gz
/Users/student2/Desktop/AO,SK_WEBSITE/Hydrogen_sulfide/H2S_DZV_vib.log.gz
      ...adding Molecular_Vibration_at_2700_Wavenumbers.spt
  ...jmolApplet9
      ...adding Molecular_Vibration_at_2650_Wavenumbers.png
      ...adding Molecular_Vibration_at_2650_Wavenumbers.spt
  ...jmolApplet10
      ...adding Molecular_Vibration_at_1320_Wavenumbers.png
      ...adding Molecular_Vibration_at_1320_Wavenumbers.spt
  adding JmolSpin.js